How to measure risk: Methodologies and Calculations

How to measure risk?

In the dynamic world of finance and investment, understanding and effectively managing risk are essential for achieving long-term success. Measuring risk involves evaluating the potential uncertainties and downside exposures associated with an investment, enabling investors to make informed decisions and construct well-balanced portfolios. In this article, we delve into various methodologies used to measure risk, providing detailed explanations and practical examples to illuminate each approach.

Standard Deviation

Standard deviation is a statistical measure that quantifies the amount of variation or dispersion of a set of values from their mean. In simpler terms, it tells you how much the individual data points in a set differ from the mean (average) of the data set. In investment analysis, standard deviation is commonly used to measure the volatility of returns, providing insights into the potential fluctuations in an investment’s performance. It is also known as unsystematic risk.

Here’s how standard deviation is calculated:

• Calculate the mean (average) of the data set.
• For each data point, find the difference between that data point and the mean.
• Square each of these differences.
• Find the mean of those squared differences.
• Take the square root of that mean.

The formula for standard deviation, denoted by the symbol σ (sigma) is

Where:

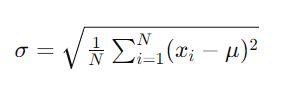
• $N$ is the number of data points in the population.
• xi​ represents each individual data point.
• $\mu$ is the mean of the data set.

Example

Let’s illustrate this with an example:

Suppose you have a set of test scores: 70, 80, 85, 90, and 95.

1. Calculate the mean: (70 + 80 + 85 + 90 + 95) / 5 = 84.
2. Find the differences from the mean: (70-84), (80-84), (85-84), (90-84), (95-84) = -14, -4, 1, 6, 11.
3. Square each difference: 196, 16, 1, 36, 121.
4. Find the mean of the squared differences: (196 + 16 + 1 + 36 + 121) / 5 = 74.8.
5. Take the square root of the mean: √74.8 ≈ 8.65.

So, the standard deviation of the test scores is approximately 8.65.

This tells you that on average, the test scores deviate from the mean by about 8.65 points. A smaller standard deviation indicates that the data points are closer to the mean, while a larger standard deviation indicates that the data points are more spread out from the mean.

Beta

In finance, beta also known as the systematic risk, is a measure of a stock’s volatility in relation to the broader market. It is used to assess the risk associated with a particular stock or portfolio compared to the overall market. Beta measures the sensitivity of a stock’s returns to changes in the market returns.

The beta coefficient is calculated using statistical methods, particularly regression analysis, comparing the stock’s returns to the returns of a benchmark index, often the market index like the S&P 500. A beta of 1 indicates that the stock’s price tends to move in line with the market. A beta greater than 1 suggests that the stock is more volatile than the market, while a beta less than 1 suggests that the stock is less volatile than the market.

Here are the interpretations of different beta values:

• Beta = 1: The stock has the same volatility as the market. For example, if the market goes up by 1%, the stock, on average, also goes up by 1%, and vice versa.
• Beta > 1: The stock is more volatile than the market. For example, if the market goes up by 1%, the stock tends to go up by more than 1%, and vice versa.
• Beta < 1: The stock is less volatile than the market. For example, if the market goes up by 1%, the stock tends to go up by less than 1%, and vice versa.

Here’s an example to illustrate beta:

Let’s say we have a stock XYZ with a beta of 1.5. If the market (represented by the S&P 500 index) goes up by 2%, we would expect XYZ to go up by approximately 3% (1.5 times 2%). Similarly, if the market goes down by 2%, we would expect XYZ to go down by approximately 3%.

On the other hand, if we have another stock ABC with a beta of 0.8, if the market goes up by 2%, we would expect ABC to go up by approximately 1.6% (0.8 times 2%), and if the market goes down by 2%, we would expect ABC to go down by approximately 1.6%.

Investors use beta to assess the risk of individual stocks or portfolios. Stocks with higher beta are considered riskier investments because they tend to experience larger price fluctuations. Conversely, stocks with lower beta are considered less risky because their prices are less sensitive to market movements.

Value at Risk (VaR)

Value at Risk (VaR) is a statistical measure used to quantify the potential loss in the value of a portfolio or investment over a specific time period and with a certain level of confidence. It provides an estimate of the maximum loss that a portfolio could suffer within a given time frame under normal market conditions.

VaR is typically expressed as a monetary amount and is associated with a probability level and a time horizon. For example, a VaR of $1 million with a confidence level of 95% over a one-day time horizon means that there is a 5% chance that the portfolio will incur losses exceeding $1 million within a single trading day under normal market conditions.

There are several methods for calculating VaR, including historical simulation, variance-covariance (parametric) method, and Monte Carlo simulation. Each method has its strengths and weaknesses, and the choice of method depends on factors such as the complexity of the portfolio and the availability of data.

Sharpe Ratio

The Sharpe Ratio is a measure used to evaluate the risk-adjusted return of an investment or a portfolio. It assesses the return earned in excess of the risk-free rate per unit of volatility or total risk. In essence, it quantifies the return achieved per unit of risk taken. A higher Sharpe Ratio indicates better risk-adjusted performance.

The formula for calculating the Sharpe Ratio is as follows:

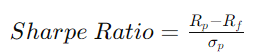
Where:

• Rp​ is the expected return of the investment or portfolio,
• Rf​ is the risk-free rate of return (typically the return on government bonds or Treasury bills),
• σp​ is the standard deviation of the investment’s or portfolio’s returns, representing its volatility.

A higher Sharpe Ratio indicates better risk-adjusted performance, as it signifies a higher return for the amount of risk taken. Conversely, a lower Sharpe Ratio suggests lower return relative to the risk involved.

Example

Suppose an investor is considering two investment options: Option A and Option B.

• Option A has an expected return of 10% and a standard deviation of 15%.
• Option B has an expected return of 8% and a standard deviation of 10%.

Assume the risk-free rate of return is 3%.

Calculating the Sharpe Ratio for each option:

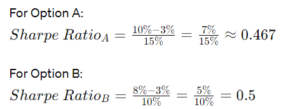
In this case, Option B has a higher Sharpe Ratio (0.5) compared to Option A (0.467), indicating that Option B provides better risk-adjusted returns. This means that Option B generates a higher return per unit of risk compared to Option A.

The Sharpe Ratio helps investors compare different investment opportunities and assess whether the returns generated by an investment adequately compensate for the level of risk undertaken. It is an essential tool in portfolio management and investment decision-making, enabling investors to optimize their risk-return trade-offs.

Scenario Analysis

Scenario analysis is a technique used in financial modeling and risk management to evaluate the potential outcomes of various scenarios under different conditions. It involves assessing the impact of different hypothetical events or changes in variables on the performance or value of an investment, project, or portfolio.

Scenario analysis involves evaluating the potential impact of different hypothetical scenarios on investment returns. By simulating various market conditions and events, investors can assess how changes in economic, political, or industry-specific factors may affect the risk profile of an investment.

Scenario analysis typically involves three main steps:

1. Identifying relevant scenarios: This step involves identifying and defining the different scenarios or potential events that could affect the investment or project. These scenarios could include changes in economic conditions, market trends, regulatory changes, or other factors specific to the investment.
2. Developing assumptions: For each scenario, assumptions are made regarding how the relevant variables would change and how they would impact the investment or project. These assumptions are often based on historical data, expert judgment, market research, or other sources of information.
3. Analyzing outcomes: Once the assumptions for each scenario are defined, the impact on key performance indicators or financial metrics is analyzed. This could include measures such as revenue, expenses, cash flow, profitability, or the value of the investment or project.

Scenario analysis helps decision-makers understand the potential risks and opportunities associated with different scenarios and make more informed decisions. It allows them to assess the sensitivity of their investments or projects to changes in key variables and develop strategies to mitigate risks or capitalize on opportunities.

Conclusion

Measuring risk is a crucial aspect of investment analysis, enabling investors to make informed decisions and construct well-diversified portfolios. By utilizing a combination of quantitative metrics and qualitative assessments, investors can gain a comprehensive understanding of the potential uncertainties and downside risks associated with their investments. Whether it’s through standard deviation, beta, VaR, Sharpe Ratio, or scenario analysis, mastering risk measurement is essential for navigating the complexities of financial markets and achieving long-term investment success.